Lines and Angles - Brain Teaser
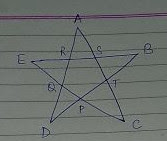
Q: What is the measure of ∠A + ∠B + ∠C + ∠D + ∠E in the figure given below, assuming no angles and sides are equal. Give reason to your answer.
Answer:
In △ BDR
∠B + ∠D + ∠R = 180° (Angle sum property of triangle)
⇒ ∠B + ∠D = 180° - ∠R .... (1)
In △ AQC
∠A + ∠C + ∠Q = 180°
⇒ ∠A + ∠C = 180° - ∠Q .... (2)
In △ CSE
∠C + ∠S + ∠E = 180°
⇒ ∠C + ∠E = 180° - ∠S .... (3)
In △ DAT
∠D + ∠A + ∠T = 180°
⇒ ∠D + ∠A = 180° - ∠T .... (4)
In △ EBP
∠E + ∠B + ∠P = 180°
⇒ ∠E + ∠B = 180° - ∠P .... (5)
Adding equations (1), (2), (3), (4) and (5)
(∠B + ∠D) + (∠A + ∠C) + (∠C + ∠E) + (∠D + ∠A) + (∠E + ∠B) = 180°×5 - ∠R - ∠Q - ∠S - ∠T - ∠P
2∠A + 2∠B + 2∠C + 2∠D + 2∠E = 900 - (∠P + ∠Q + ∠R + ∠S + ∠T)
2(∠A + ∠B + ∠C + ∠D + ∠E) = 900 -540 (Sum of interior angles of a pentagon is 540°)
∠A + ∠B + ∠C + ∠D + ∠E = 360 ÷ 2
∠A + ∠B + ∠C + ∠D + ∠E = 180°

No comments:
Post a Comment
We love to hear your thoughts about this post!
Note: only a member of this blog may post a comment.