Playing With Numbers
EXERCISE 3.5
CBSE Class 6 Maths
Q1: Which of the following statements are true?
(a) If a number is divisible by 3, it must be divisible by 9.
(b) If a number is divisible by 9, it must be divisible by 3.
(c) A number is divisible by 18, if it is divisible by both 3 and 6.
(d) If a number is divisible by 9 and 10 both, then it must be divisible by 90.
(e) If two numbers are co-primes, at least one of them must be prime.
(f) All numbers which are divisible by 4 must also be divisible by 8.
(g) All numbers which are divisible by 8 must also be divisible by 4.
(h) If a number exactly divides two numbers separately, it must exactly divide their sum.
(i) If a number exactly divides the sum of two numbers, it must exactly divide the two numbers separately.
Answer:
(a) ✗ (e.g. 15 is divisible by 3 but not by 9)
(b) ✔
(c) ✔
(d) ✔
(e) ✗ (e.g. 8 and 9 are co-primes and none of these are prime. )
(f) ✗
(g) ✔
(h) ✔
(i) ✗
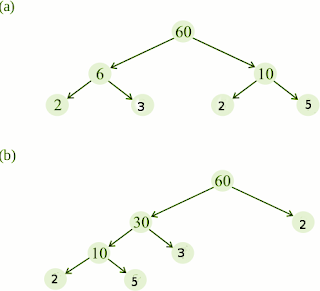
Q2: Here are two different factor trees for 60. Write the missing numbers.
Answer:
Q3: Which factors are not included in the prime factorisation of a composite number?
Answer: 1 is not included in the prime factorisation of a composite number. (∵ 1 is neither prime nor composite)
Q4: Write the greatest 4-digit number and express it in terms of its prime factors.
Answer: The greatest 4-digit number = 9999
9999
↙ ↘
3 3333
↙ ↘
3 1111
↙ ↘
11 101
∴ The prime factors of 9999 = 3 × 3 × 11 × 101
Q5: Write the smallest 5-digit number and express it in the form of its prime factors.
Answer: The smallest five digit number is 10000.
10000
↙ ↘
2 5000
↙ ↘
2 2500
↙ ↘
5 500
↙ ↘
5 100
↙ ↘
5 20
↙ ↘
5 4
↙ ↘
2 2
The prime factors of 10000 are 2 × 2 × 2 × 2 × 5 × 5 × 5 × 5.
Q6: Find all the prime factors of 1729 and arrange them in ascending order. Now state the relation, if any; between two consecutive prime factors.
Answer: Prime factors of 1729 = 7 × 13 × 19
The difference of any two consecutive prime numbers = 6
i.e. 13 - 7 = 6, 19 - 13 = 6
Q7: The product of three consecutive numbers is always divisible by 6. Verify this statement with the help of some examples.
Answer: Among the three consecutive numbers, at least one number is even and one is multiple of 3. Thus, the product must be multiple of 6.
e.g.
2 × 3 × 4 = 24
6 × 7 × 8 = 336
Q8: The sum of two consecutive odd numbers is divisible by 4. Verify this statement with the help of some examples.
Answer:
3 + 5 = 8 and 8 is divisible by 4.
5 + 7 = 12 and 12 is divisible by 4.
7 + 9 = 16 and 16 is divisible by 4.
9 + 11 = 20 and 20 is divisible by 4
Q9: In which of the following expressions, prime factorisation has been done?
(a) 24 = 2 × 3 × 4
(b) 56 = 7 × 2 × 2 × 2
(c) 70 = 2 × 5 × 7
(d) 54 = 2 × 3 × 9
Answer:
(a) ✗ ∵ 4 is not a prime factor.
(b) ✔
(c) ✔
(d) ✗ ∵ 9 is not a prime factor.
Q10: Determine if 25110 is divisible by 45.
[Hint : 5 and 9 are co-prime numbers. Test the divisibility of the number by 5 and 9].
Answer:
Prime factors of 45 = 5 × 9
25110 is divisible by 5 as ‘0’ is at its unit place.
25110 is divisible by 9 as sum of digits (2+5+1+1+0 = 9) is divisible by 9.
∴ the number must be divisible by 5 × 9 = 45
Q11: 18 is divisible by both 2 and 3. It is also divisible by 2 × 3 = 6. Similarly, a number is divisible by both 4 and 6. Can we say that the number must also be divisible by 4 × 6 = 24? If not, give an example to justify your answer.
Answer: No. Number 12 is divisible by both 6 and 4 but 12 is not divisible by 24.
Q12: I am the smallest number, having four different prime factors. Can you find me?
Answer: The smallest four prime numbers are 2, 3, 5 and 7.
Hence, the required number is 2 × 3 × 5 × 7 = 210


No comments:
Post a Comment
We love to hear your thoughts about this post!
Note: only a member of this blog may post a comment.