CBSE Class 11 - Physics - Gravitation - Kepler's Laws (#cbseNotes)

Kepler's Laws

Class 11 - Physics - Gravitation 

Kepler's Laws

There has always been a great interest in the motion of planets. Part of the reason is that some people believe that it changed the course of science and laid foundation to Newtonian Laws. By 16th century, a lot of data on the motion of planets had been collected by many astronomers. Based on that data Johannes Kepler, after a life time study, worked out three empirical laws which govern the motion of planets and are known as Kepler's laws of planetary motion.

The laws for planets orbiting the sun, they hold equally well for satellites, either natural or artificial, orbiting Earth or any other massive central body.

The three laws are:

① The law of orbits
② Law of areas
③ Law of periods




1. The law of orbits:
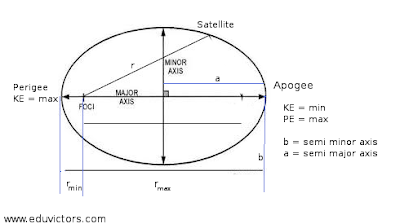
Each planet revolves about the sun in an elliptical orbit with the sun at one of the foci of the ellipse.

A planet of mass m moving in an elliptical orbit around the sun. The sun, of mass M, is at one focus S of the ellipse. The other focus S', which is located in empty space. Each focus is a distance ea from the ellipse's centre, with e being the eccentricity of the ellipse. The semi-major axis a of the ellipse, the perihelion (nearest the sun) distance rₘiₙ, and the aphelion (farthest from the sun) distance rₘₐₓ are also shown.

rₘₐₓ = a + ea = (1+e)a
rₘiₙ = a - ea = (1-e)a

The distance of each focus from the center of the ellipse is ea, where e is the dimensionless number between 0 to 1 called the eccentricity. If e = 0, the ellipse is a circle. For earth e = 0.017.


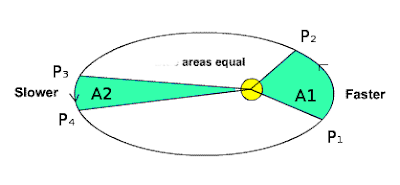
2. Law of areas:
An imaginary line that connects a planet to the sun sweeps out equal areas in the plane of the planet's orbit in equal times, i.e. the rate dA / dt at which it sweeps out area A is constant.

If tP1P2 = tP3P4 then A1 = A2

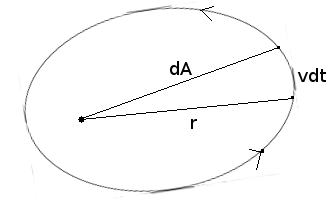
dA     (r)(vdt)     rv
--- = ---------- = ----   and as L = mvr 
dt       2dt        2

so dA / dt = L/2m

But as L = constant, (force is central so torque is zero, therefore angular momentum of the planet is conserved) areal velocity (dA / dt) = constant which is Kepler's II law or constancy of areal velocity is a consequence of conservation of angular momentum.

Note: Kepler’s laws are valid for satellites also.

3. Law of periods:
The square of the period of revolution of any planet is proportional to the cube of the semi-major axis of the orbit, i.e. T² α r³.

The squares of the periods of the planets are proportional to the cube of their mean distances from the sun.

where a = semi-major axis,
   r₁ = Shortest Distance of planet from the Sun (perigee)
   r₂ = Largest Distance of planet from the Sun (apogee)