CBSE Class 9 - Maths - Quadrilaterals (Worksheet-4) (#class9Maths)(#eduvictors)

Class 9 - Maths - Quadrilaterals (Worksheet-4)

Q1: ABCD is a parallelogram such that its diagonals are equal. What is the measure of ∠ABC?

Answer: Since diagonals are equal, it must be a rectangle or a square. ∴ ∠ABC = 90°

Q2: Is rhombus a kite or a parallelogram?

Answer: Both

Q3: In a parallelogram ABCD, if ∠C = 80° then what is the measure of ∠A? 

Answer: In a parallelogram, opposite angles are equal, ∴ ∠A = ∠C = 80°

Q4: Each diagonal divides the parallelogram into two _________ triangles. (Fill in the blanks)

Answer: congruent

Q5: In a parallelogram ABCD, if ∠A is 4/5 of ∠B, then what is ∠A? 

Answer: In a parallelogram adjacent angles are supplementary. 

Q6: Three angles of a quadrilateral are respectively equal to 110°, 50° and 40°. Find its fourth angles.

Answer: Let the measure of the fourth angles be x°. We know that the sum of the angles of a quadrilateral is 360°.

∴  110° +  50° +  40° + x° = 360°

      x = 360 - 200 = 160°    (Answer)

Q7: Each side of a rhombus is 15 cm. if the length of one of its diagonals is 18 cm, then what is the length of the other diagonal? 

Answer: In a rhombus diagonals are ⊥ bisectors. As shown in figure, △AOB is a rt. angle △.

Applying Pythagoras theorem,

      AB² = BO² + AO²

      15² = BO² + 9²

      BO² = 225 - 81 = 144

      BO = 12

      BD = 2 × 12 = 24cm 

Q8: Two opposite angles of a parallelogram are (3x − 2)° and (50 − x)°. Find the the value of x.

Answer: Opposite angles of a parallelogram are equal.      

∴  (3x − 2)° = (50 − x)°

     3x + x = 50 + 2

     4x = 52

     x = 52 / 4 =  13°  (Answer) 

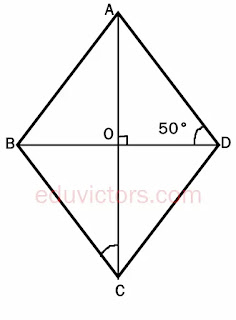
Q9: ABCD is a rhombus such that ∠ADB = 50°, then what is the measure of ∠ACB?

Answer:  In a rhombus diagonals are ⊥ bisectors. As shown in figure, △AOD is a rt. angle △.

Using Angle sum property of △.  ∠DAC = 40°

∵ AD ∥ BC 

∴  ∠ACB = ∠DAC = 40°    (al. interior angles are equal).

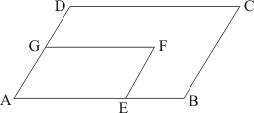
Q10: In the given figure, ABCD and AEFG are two parallelograms. If ∠C = 58°, find ∠F.

Answer: The opposite angles of a parallelogram are equal.

In ∥gm ABCD,  ∠A = ∠C = 58°

In ∥gm AEFG,  ∠F = ∠A = 58°      (opp. angles are equal)

👉See Also:

CH 8 Quadrilaterals
CH 8 Quadrilaterals (NCERT Ex 8.1) 
CH 8 Quadrilaterals (NCERT Ex 8.2)
CH 8 Quadrilaterals (Important Points To Remember)
CH 8 Quadrilaterals (Problems and Solutions)
CH 8 Quadrilateral (Worksheet-1)
Understanding Quadrilaterals (Worksheet-2)
Understanding Quadrilaterals (MCQs)
10 Parallelogram Theorems You Must Know!

Quadrilaterals (Properties)
Types of Quadrilaterals (Worksheet-3)