CBSE Class 10 Maths - Quadratic Equations - Nature of Roots (Solved Problems)
We know that A polynomial p(x) = ax² + bx + c of degree 2 is called a quadratic polynomial, then p(x) = 0 is known as quadratic equation.
There are three methods to find the solution of a quadratic equation:
1. Factorisation method
2. Method of completing the square
3. Quadratic formula method
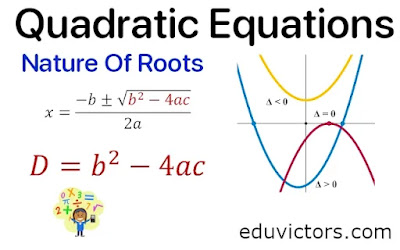
What is a Discriminant of Quadratic Equation ax² + bc + c = 0 ?
In general, Discriminant is represented by symbol D.
Mathematically,
D = $D = b^2 - 4ac$
The Discriminant helps us find the nature of roots.
⑴ If D > 0 i.e. $b^2 - 4ac > 0$ then the given quadratic equation (QE) has two distinct real roots. (Note: Distinct mean unique values, real mean real numbers).
Value of roots will be :
$x = \frac{-b + \sqrt{D}}{2a}$ and $x = \frac{-b - \sqrt{D}}{2a}$
⑵ If D = 0 i.e. $b^2 - 4ac > 0$ then the QE has equal real roots.
i.e. $x = \frac{-b}{2a}$ and $x = \frac{-b}{2a}$
⑶ If D < 0 then $\sqrt{D} = \sqrt{-ve }$, there is no real roots exist.
We can say roots are imaginary or complex numbers (that you'll study in Class XI).
Sum of Roots of a quadratic equation:
For real roots, α = $\frac{-b + \sqrt{D}}{2a}$ and β = $\frac{-b - \sqrt{D}}{2a}$
Now α + β = \frac{-b + \sqrt{D}}{2a} +\frac{-b - \sqrt{D}}{2a}$
= $\frac{-b + \sqrt{D} -b - \sqrt{D}}{2a} $
= $\frac{-2b}{2a} $
= $\frac{-b}{a}$
Product of roots of a quadratic equation:
For real roots, α = $\frac{-b + \sqrt{D}}{2a}$ and β = $\frac{-b - \sqrt{D}}{2a}$
Now α × β = $\frac{-b + \sqrt{D}}{2a} \times \frac{-b - \sqrt{D}}{2a} $
= $\frac{(-b)^2 - (\sqrt{D})^2}{4a^2} $
= $\frac{b^2 - D}{4a^2} $
= $\frac{b^2 -b^2 + 4ac}{4a^2}$
= $\frac{4ac}{4a^2}$
= $\frac{c}{a}$
For a quadratic equation ax² + bx + c = 0,
ⅰ If sum of roots is 0, then b = 0
ⅱ If roots are reciprocal of each other then a = c
ⅲ If products of roots is 0, then c = 0.
Q1: Write the discriminant of each of the following quadratic equations. Find the nature of roots also.
x² + 4x + 3 =0
Answer: D = b² - 4ac
In the given QE, a = 1, b = 4, c = 3
∴ D = 4² - 4(1)(3)
D = 16 - 12
D = 4
∵ D > 0, roots are distinct and real.
Q2: Write the discriminant of each of the following quadratic equation:
2x² + 4x + 5 = 0
Answer: In the given QE, a = 2, b = 4 and c = 5
D = b² - 4ac
∴ D = 4² - 4(2)(5)
D = 16 - 40
D = -24
∵ D < 0, roots are non-real or imaginary.
Q3: Write the discriminant of each of the following quadratic equations and also find the nature of roots.
$\sqrt{3}x^2 -2\sqrt{2} - 2\sqrt{3} = 0$
Answer: In the given quadratic equation, a = $\sqrt{3}$, b = $-2\sqrt{2}$ and c = $- 2\sqrt{3}$
D = b² - 4ac
∴ D = $(-2\sqrt{2})^2 - 4(\sqrt{3})(- 2\sqrt{3})$
= 8 - (-24)
= 8 + 24
= 32
∵ D > 0, roots are distinct and real.
Q4: Write the discriminant of each of the following quadratic equations and also find the nature of roots.
x² + 6x + 9 = 0
Answer:
In the given QE, a = 1, b = 6 and c = 9
D = b² - 4ac
∴ D = 6² - 4(1)(9)
D = 36 - 36
D = 0
∵ D = 0, roots are real and equal.
Q5: Find the value of k, so that the quadratic equation
(k + 1) x² – 2 (k — 1) x + 1 = 0 has equal roots.
Answer: In the given QE,
a = k + 1, b = -2(k - 1) and c = 1
For equal roots Disrciminant D = 0
∴ D = b² - 4ac = 0
⇒ (-2(k - 1))² - 4(k + 1)(1) = 0
4(k-1)² - 4k - 4 = 0
4[(k-1)² -k - 1] = 0
4[k² -2k + 1 -k -1] = 0
4[k² -3k] = 0
⇒ 4k(k-3) = 0
⇒ 4 ≠ 0, k = 0 or k - 3 = 0
⇒ k = 0 or k = 3
∴ Values of k are 0, 3
CH 4: Quadratic Equations (NCERT Ex 4.2)
CH 4: Quadratic Equations (Summary)
CH 4: 10 Question Patterns Commonly Asked in Question Paper
No comments:
Post a Comment
We love to hear your thoughts about this post!
Note: only a member of this blog may post a comment.