Class 11 - Maths - Chapter: Sets - Operations Of Sets (#class11Maths)(#eduvictors)

Sets - Operations Of Sets

Class 11 - Maths

COMPLEMENT OF A SET

If U  be the universal set and A is the subset of U, then the complement of A with respect to U, denoted by A',
A' is defined as
A' = {x : x ∈ U and x  ∉ A }



i.e. the complement of A is the set of those elements of U which are not elements of A.

OPERATIONS OF SETS

Main set operations are:
i.   Union of Sets
ii.  Intersection of Sets
iii. Difference of Sets


UNION OF TWO SETS
The union of any two given sets A and B is the set C which consists of all those elements which are either in A or in B.
Symbolically, we write
C = A ∪ B = {x | x ∈A or x ∈B}

Example:
A = {1,2,3,4} and B = {2,4,6,8}
A ∪ B = {1,2,3,4,6,8}

Some properties of the operation of union are:
(i) A ∪ B = B ∪ A
(ii) (A ∪ B) ∪ C = A ∪ (B ∪ C)
(iii) A ∪ φ = A
(iv) A ∪ A = A
(v) U ∪ A = U


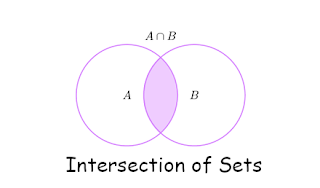
INTERSECTION OF SETS
The intersection of two sets A and B is denoted by A ∩ B i.e. it is the set which consists of all those elements which belong to both A and B.
Symbolically, we write
A ∩ B = {x : x ∈ A and x ∈ B}.

Example:
A = {2,4,6,8}  and B = {6, 8, 10, 12}
A ∩ B = {6, 8}

DISJOINT SETS
Two sets A and B are said to be disjoint if,  A ∩ B = φ
e.g. A = {1,2,3,4} and B = {6,7,8} then A ∩ B = φ. Its Venn diagram representation is:

Some properties of the operation of intersection
(i) A ∩ B = B ∩ A
(ii) (A ∩ B) ∩ C = A ∩ (B ∩ C)
(iii) φ ∩ A = φ ; U ∩ A = A
(iv) A ∩ A = A
(v) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
(vi) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)


DIFFERENCE OF TWO SETS
Difference of two sets is denoted by A - B. is defined as set of elements which belong to A but not to B. Symbolically,
A – B = {x : x ∈ A and x ∉ B}
    also, B – A = { x : x ∈ B and x ∉A}

Examples:
A = {1, 2, 3, 4, 6, 12} and B = {1, 2, 4, 8, 16}
A - B = {3, 6, 12}
B - A = {8, 16}



☛See also:
Special Mathematical Constants

 SETS (NCERT Ex 1.1)
 SETS (NCERT Ex 1.2)
 Different Types of Sets
 SETS (NCERT Ex 1.3)

 SETS (Unit Test Paper)
SETS (VENN DIAGRAMS)