Class 10 Maths - Revision Assignment - 1 (1 - Mark Questions - Answers) (#class10Maths)(#cbse2020)(#eduvictors)

Class 10 Maths - Revision Assignment - 1

Chapters covered: Real Numbers, Polynomials, Arithmetic progressions, Co-ordinate Geometry, Introduction to Trigonometry

1-Mark based Questions (with Answers)

Q1: What is the HCF of the smallest composite number and the smallest prime number?

Answer: Smallest composite number = 4

    Smallest prime number = 2

    HCF (4, 2) = 2

Q2: If HCF of a and b is 12 and product of these numbers is 1800. What is the LCM of these numbers?

Answer: a × b = HCF × LCM 

 ⇒ 1800 = 12 × LCM

 ⇒ LCM = 1800 / 12 = 150

Q3:  Find the quadratic polynomial whose zeros are -3 and 4

Answer: Sum of zeros (α + β) = -3 + 4 = 1

     Product of zeros (α β) = -3×4 = -12

     p(x) = k[x² - (α + β)x +  α β]

     

     for k = 1

     p(x) = x² -x - 12

 

Q4:  If both zeros of a quadratic polynomial ax² + bx + c are equal and opposite in sign, then find the value of b.

Answer: Let roots be α  and -α 

       Sum of roots = α  - α  = 0 = -b/a

       ⇒ b = 0

Q5: The first term of an AP is p and its common difference is q. Find its 10th term.

Answer: a₁₀ = a + 9d = p +9q

Q6:  If aⁿ = 5 - 11n, find the common difference

Answer: Here d =  aⁿ⁺¹ - aⁿ  

= 5 - 11(n + 1) - (5 - 11n) = 5 - 11n  - 11 -5 + 11n  = -11

Q7: Find the distance between (0, 5) and (-5, 0)

Answer: 

  Here x₁  = 0,    y₁  = 5
           x₂  = -5,  y₂  = 0	   
       _____________________
  d = √(x₂ - x₁)² + (y₂ - y₁)²

       _____________________
  d = √(-5 - 0)² + (0 - 5)²

  d = √(25 + 25)  = √(50) = 5√2 units

  
  

Q8: AOBC is a rectangle whose three vertices are A (0, 3), B(5,0), O(0,0). Find the length of its diagonal.

Answer:  

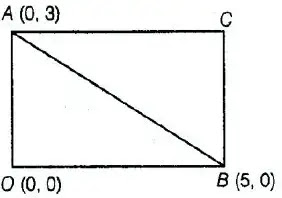
    AB = √(5 - 0)² + (0 - 3)²        
           _______    ____
        = √25 + 9  = √(34)

  

Q9: Write the acute angle θ satisfying (√3) sinθ = cos θ

Answer:(√3) sinθ = cos θ

     tan θ = 1/(√3) = tan 30°

   ⇒  θ =  30°

Q10: What is the maximum value of 1/sec θ, where 0° ≤ θ ≤ 90°

Answer: ∵ sec θ is in denominator, 

∴ minimum value of sec θ will return maximum value of 1/sec θ.

Min. value of sec θ = sec 0° = 1

Thus max value of 1/sec θ = 1/1 = 1

👉See Also:

CH 2: Polynomials (Study Points)

CH 1: Real Numbers (Important Formulae and Key Points)
CH 1: Real Numbers (Typical HCF & LCM related Problems)

CH 5: Arithmetic Progressions (MCQs)  

CH 8: Introduction to Trigonometry (Short Q & A)

CH7: Coordinate Geometry (1 mark Questions and Answers)