CBSE Class 11 - Mathematics - Limits and Derivatives
Part-1 - Questions and Answers
Q1: Define Calculus.
Answer: Calculus is that branch of mathematics that mainly deals with the study of change in the value of a function as the points in the domain change.
👉Note: The chapter "Limits and Derivatives" is an introduction to Calculus.
👉Calculus is a Latin word meaning ‘pebble’. Ancient Romans used stones for counting.
Q2: Who are called pioneers of Calculus (who invented Calculus)?
Answer: Issac Newton (1642 - 1727) and G. W. Leibnitz(1646 - 1717).
Both of them were invented independently around the 17th century.
Q3: What is the meaning of 'x tends to a' or x → a?
Answer: When x tends to a (x → a), x is nearly close to a but never equals to a.
e.g. x → 3 means the value of x maybe 2.99 or 2.999 or 2.999...9 is very close to 3 but not exactly equal to 3. Similarly, x may be 3.01, 3.001, 3.0001... from the right side and gets closer to 3.
Q4: What do you mean by the left limit of f(x) and right limit of f(x)?
Answer: Consider a function f(x) = x²
Thus at x = 2, f(2) = 4.
When x is less than 2 but increases and gets closer to 2, f(x) also gets closer to 4.
Thus we say x approaches to 2 from left or f(x) approaches 4.It is called the left-limit of f(x) as x → a is l. If f(x) is arbitrarily close to l when x is in the left-deleted neighbourhood of a and close to it.
Symbolically, $\lim_{x\rightarrow a^-} f(x) = l$ or f(a⁻) = l.
Similarly, when x is greater than 2 and is decreasing and getting closer to 2, f(x) also goes closer to 4.
We can say x approaches 2 from the right, f(x) approaches 4 from the above.
It is called the right limit of f(x) as x → a is l. If f(x) is arbitrarily close to l when x is in the right-deleted neighbourhood of a and close to it.
Symbolically, $\lim_{x\rightarrow a^+} f(x) = l$ or f(a⁺) = l.
Q5: Given function f(x) = x + 5. Find the limit x → 2
Is the function continuous?
Answer: Let us prepare a table when x approaches 2 from left as well as from right.
As the table shows, the value of f(x) at x = 2 is greater than 6.999 and less than 7.001.
⇒ $\lim_{x\rightarrow 2^-} f(x) = 7$ and $\lim_{x\rightarrow 2^+} f(x) = 7$
Hence $\lim_{x\rightarrow 2} f(x) = 7$
Yes, the function is continuous.
Q6: Some rational functions give rise to meaningless conditions like $\frac{0}{0}$. How can we handle such conditions?
Answer: Using limits. It can be solved by cancelling out the factor that is giving 0 by both numerator and denominator
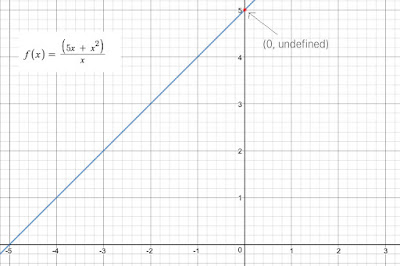
Q7: Find the limit as x → 0 for $f(x) = \frac{5x + x^2}{x}$
Answer: At x = 0, f(x) = $\frac{0}{0}$, which is meaningless.
It implies
$f(x) = \left\{\begin{matrix} 5 + x, \text{if } x \neq 0 \\ \text{is undefined if x = 0} \end{matrix}\right.$
Function f(x) is not continuous at x = 0.
$ f(x) = \lim_{x\rightarrow 0} \frac{5x + x^2}{x} $
$ f(x) = \lim_{x\rightarrow 0}\frac{x(5 + x)}{x} $
$ f(x) = \lim_{x\rightarrow 0} 5 + x = 5$
Thus limit as x approaches 0, f(x) is 5.
Q8: What are three conditions be true then we can say function f is continuous?
Answer: A function f is said to be continuous at x = a if and only if three conditions are all satisfied:
1. f(a) is defined,
2. $\lim_{x\rightarrow a}$ exists
3. f(a) = $\lim_{x\rightarrow a}f(x)$
Q9: Are there any conditions for a function where a limit does not exist? Explain with an example.
Answer: Yes.
Consider f(x) = $\lim_{x\rightarrow 0} (\frac{-1}{x}) $
For x = -0.5, f(x) = 2,
x = -0.1, f(x) = 10,
x = -0.01, f(x) = 100
x = -0.001, f(x) = 1000,
x = 0.5, f(x) = -2
x = 0.1, f(x) = -10,
x = 0.01, f(x) = -100
x = 0.001, f(x) = -1000,
Here LHL ≠ RHL.
The values are not approaching a limit, the limit does not exist.
SETS (VENN DIAGRAMS)
SETS (Operations of Sets)
SETS (NCERT Ex 1.4 Q1-Q5)
SETS (NCERT Ex 1.4 Q6 - Q8)
SETS (NCERT Ex 1.4 Q9 - Q12)
SETS (NCERT Ex 1.5)
SETS (NCERT Ex 1.6)
Laws of Set Operations
Ch2: Relations and Functions (1 Mark Q & A) Part-1
Ch2: Cartesian Product of Two Sets (Important Points)
Ch2: Relations - Domain, Range and Co-Domain (Solved Problems)
Ch5: Complex Numbers (Part 1) - Solved Problems
Maths Annual Test Paper (2018-19)
Maths Annual Test Paper (2020-21)
Maths Term1 MCQs (2021-22)




No comments:
Post a Comment
We love to hear your thoughts about this post!
Note: only a member of this blog may post a comment.