CBSE Class 11 Maths - Relations - Domain, Range and Co-Domain
RELATION
Let A and B be two nonempty sets. Then, a relation R from A to B is a subset of (A × B).
Thus, R is a relation from A to B ⇔ R ⊆ (A × B).
If (a, b) ∈ R then we say that ‘a is related to b‘ and we write, a R b.
If (a, b) ∉ R then ‘a is not related to b‘ and we write, $a \not \mathrel{R} b$.
Q1: Let A = {-1, 2, 4} and B = {1, 3}. Show A × B as arrow diagram.
Answer: A × B = {(-1,1), (-1, 3), (2,1), (2,3), (4,1), (4,3)}
The arrow diagram is:
DOMAIN, RANGE AND CO-DOMAIN OF A RELATION
Let R be a relation from A to B. Then, R ⊆ (A × B).
(i) The set of all first coordinates of elements of R is called the domain of R, written as dom(R).
(ii) The set of all second coordinates of elements of R is called the range of R, denoted by range(R).
(iii) The set B is called the co-domain of R.
Dom (R) = {a : (a, b) ∈ R} and Range (R) = {b : (a, b) ∈ R}.
Q2: Let A - {1,2,3,...,14}. Define relation R from A to A by R = {(x,y) : 3x - y = 0 where x, y ∈ A}.
Write down the domain, co-domain and range.
Answer: By the definition of the relation R = {(1,3) (2,6) (4,12)}
The corresponding arrow diagram is:
(ii) The domain is (set of first elements) = {1, 2, 3, 4}
(iii) Range (set of second elements) = {3, 6, 9, 12}
(iv) The co-domain is = {1, 2, 3, ... 14}
Q3: A = {1, 2, 3, 5} and B = {4, 6, 9}. Define relation R from A to B by R = {(x,y) : the difference between x and y is odd, x ∈ A, y ∈ B}.
Write R is roster form.
Answer: Here A = {1,2,3,5} and B = {4,6,9}
Relation R from A to B is given by:
R = {(x,y) : the difference between x and y is odd, x ∈ A, y ∈ B}
∴ R = {(5,4)}
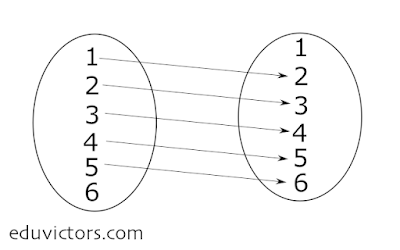
Q4: LetA= {1,2,3,4,5,6}.Define a relation R from A to A by R={(x,y):y= x+1}
(i) Depict this relation using an arrow diagram.
(ii) Write down the domain, codomain and range of R.
Answer:
(i) By the definition of the relation,
R = {(1,2), (2,3), (3,4), (4,5), (5,6)}.
(ii) The arrow diagram is:
(iii) We can see that the domain ={1, 2, 3, 4, 5,}
Similarly, the range = {2, 3, 4, 5, 6} and
the codomain = {1, 2, 3, 4, 5, 6}.
Total Number of Relations from A to B
Let n(A) = p and n(B) = q. Then, n(A B) = pq.
Since every subset of A × B is a relation from A to B. Total number of subsets of A × B is $2^{pq}$.
∴ total number of relations from A to B = $2^{pq}$ .
Q5: Let X = {a, b, c} and Y = {1, 2} . Find the number of all possible relations that can be defined from X to Y.
Answer:
Here n(X) = 3 and n(Y) = 2.
So, n(X × Y) = (3 × 2) = 6.
Since a set containing n elements has 2n subsets.
∴ (X × Y) will have 2⁶ = 64 subsets.
Since every subset of X×Y is a relation from X to Y.
Hence, there are in all 64 relations from X to Y.
👉See Also:
SETS (NCERT Ex 1.6)
Laws of Set Operations
Ch2: Relations and Functions (1 Mark Q & A) Part-1
Ch2: Cartesian Product of Two Sets (Important Points)
Maths Annual Test Paper (2018-19)



No comments:
Post a Comment
We love to hear your thoughts about this post!
Note: only a member of this blog may post a comment.