CBSE - Class 9 - Maths - CH8 - Quadrilaterals

Quadrilaterals

Simple Classification of Quadrilaterals.
For detailed version check at wikipedia

Q1: Define quadrilateral.

Answer: A quadrilateral is the union of four line-segments determined by four distinct coplanar points of which no three are collinear and the line-segments intersect only at end points.

Q2: What are the three conditions essential to construct a planar quadrilateral?

Answer: The three conditions are:

1. The four points A, B, C and D must be distinct and co-planar.
2. No three of points A, B, C and D are co-linear.
3. Line segments i.e. AB, BC, CD, DA intersect at their end points only.

Q3: What is a convex quadrilateral?

Answer: If in a given quadrilateral, no side intersects the line to its opposite side, then the quadrilateral is said to be a convex quadrilateral. The diagonals of a convex quadrilateral intersect each other.

Q4: If four points are co-linear, can it be a quadrilateral?

Answer: No. It would be a line segment.

Q5: What is the angle sum property of quadrilateral?

Answer: Sum of interior angles of a quadrilateral equals 360°.
               Sum of exterior angles of a quadrilateral equals 360°.

As shown in figure above,
sum of interior angles, ∠1 + ∠2 + ∠3 + ∠4 = 360°
and  sum of exterior angles, ∠5 + ∠6 + ∠7 + ∠8 = 360°

Q6: Prove that the sum of interior angles of a quadrilateral equals 360°.

Answer: Let ABCD be a quadrilateral and AC be a diagonal.

Using angle sum property of a triangle, in Δ ABC,

∠BAC + ∠ACB + ∠B = 180°            ...(i)

Similarly in  ΔADC,
∠DAC + ∠ACD + ∠D = 180°            ...(ii)

Adding (i) and (ii), we get
∠BAC + ∠ACB + ∠B + ∠DAC + ∠ACD + ∠D = 180° + 180°
∠BAC +  ∠DAC + ∠B + ∠ACB + ∠ACD + ∠D = 360°
∵ ∠BAC +  ∠DAC = ∠A and ∠ACB + ∠ACD = ∠A, we have
 ∠A + ∠B + ∠C + ∠D = 360°


Q7(NCERT): The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral. 

Answer: Let the common ration be p.
∴ Angles are: 3p, 5p, 9p and 13p.
Using angle sum property of quadrilateral i.e. sum of interior angles of a quadrilateral equals 360°.
⇒ 3p + 5p + 9p + 13p =  360°
⇒ 30p =  360°
⇒ p = 12°
∴ Angles are:
3p = 3 × 12° = 36° 
5p = 5 × 12° = 60° 
9p = 9 × 12° = 108° 
3p = 13 × 12° = 156° 

Q8(CBSE 2011): Angles of a quadrilateral are in the ratio 3 : 6 : 8: 13. The largest angle is :

(a) 178°
(b) 90°
(c) 156°
(d) 36°

Answer: (c) 156°
3p + 6p + 8p + 13p = 30p = 360° ⇒ p = 12° Largest angle is 13p = 13 × 12° = 156°

Q9: How will you define opposite sides of a quadrilateral?

Answer: The opposite sides of a quadrilateral are two of its sides which have no common point.

As shown in Fig-5, AB, CD form pair of opposite sides. Similarly, AD, BC form another pair of opposite sides.

Q10: What are the adjacent or consecutive sides of a quadrilateral?

Answer: The consecutive sides of a quadrilateral are two of its sides that have a common end point.
As shown in Fig-5, AD, AB for one pair of consecutive sides.
The other three pairs of consecutive sides are: (AB, BC), (BC,CD) and (CD, DA)

Q11: Identify the opposite angles in quadrilateral shown in Fig-5.

Answer: The opposite angles of a quadrilateral are two of its angles which do not include a side in their intersection.

In Fig-5, ∠A, ∠C form one pair of opposite angles. ∠B, ∠D form another pair of opposite angles.

Q12: Identify the consecutive angles in quadrilateral shown in Fig-5.

Answer: Pair of consecutive angles are: (∠A, ∠B), (∠B, ∠C), (∠C, ∠D) and (∠D, ∠A).

Q13: Three angles of a quadrilateral are 75º, 90º and 85º. The fourth angle is
(a) 90º
(b) 85º
(c) 105º
(d) 110º

Answer: (d) 110º

Q14: Define Parallelogram.

Answer: A quadrilateral which has both pairs of opposite sides parallel, is called a parallelogram.
Its properties are:

• The opposite sides of a parallelogram are equal.
• The opposite angles of a parallelogram are equal.
• The diagonals of a parallelogram bisect each other.

Q15: What is a Trapezium?

Answer:  A quadrilateral which has one pair of opposite sides parallel is called a trapezium.

Q16: What is an isosceles trapezium?

rhombus

Answer: A trapezium, in which the sides that are not parallel are equal in length and angles formed by parallel sides are equal, such trapezium is called isosceles trapezium.

Q17: What is a rhombus?

Answer: A rhombus is a parallelogram in which any pair of adjacent sides is equal.

Properties of a rhombus:

• All sides of a rhombus are equal
• The opposite angles of a rhombus are equal
• The diagonals of a rhombus bisect each other at right angles.

rectangle

Q18: What is a rectangle?

Answer:  A parallelogram which has one of its angles a right angle is called a rectangle.
Properties of a rectangle are:

• The opposite sides of a rectangle are equal
• Each angle of a rectangle is a right-angle.
• The diagonals of a rectangle are equal.
• The diagonals of a rectangle bisect each other.

Q19: What is a square?

Answer: A square is a rectangle, with a pair of adjacent sides equal.

 Or

A quadrilateral all of whose sides are equal and all of whose angles are right angles.

Or

A a parallelogram having all sides equal and each angle equal to a right angle is called a square.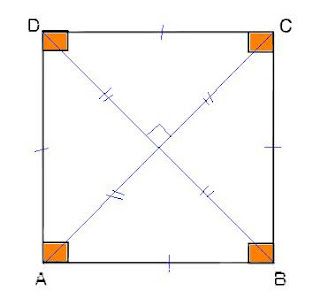

square

Properties of square are:

• All the sides of a square are equal.
• Each of the angles measures 90°.
• The diagonals of a square bisect each other at right angles.
• The diagonals of a square are equal.

Q20(CBSE 2011): All the angles of a convex quadrilateral are congruent. However, not all its sides are congruent. What type of quadrilateral is it?

(a) parallelogram
(b) square
(c) rectangle
(d) trapezium

Answer: (c) rectangle


(In progress...)